PENERAPAN IRISAN DAN GABUNGAN DALAM KEHIDUPAN
1. Dalam suatu kelas terdapat 40 siswa. Sebanyak 24 siswa gemar bermain tenis, 23 gemar bermain sepak bola dan 11 siswa gemar kedua-duanya.Gambarlah diagram venn dari keterangan di atas!
Tentukan:
Banyak siswa yang hanya gemar bermain tenis.
Banyak siswa yang hanya gemar bermain sepak bola.
Banyak siswa yang tidak gemar kedua-duanya.
SOLUSI:
Diketahui:
S = 40
Tenis ada 24
Sepak bola ada 23
Irisan = 11
Dit:
Diagram venn
n (Tenis), n (sepak bola) dan tidak gemar keduanya (x).
Isikan terlebih dahulu irisannya yaitu 11.
n (tenis) diisi dengan 24-11 =
13.
n (sepak bola) diisi dengan 23-11 = 12.
X (ditulis di luar kurva)
x =40-(13+11+12)
x =40-36
x =4
Berarti:
13 siswa hanya gemar tenis
12 siswa hanya gemar sepak bola
4 siswa tidak gemar keduanya
2. Dari sekelompok anak diperoleh data 45 orang suka makan bakso, 34 orang suka makan mie ayam 23 orang suka makan bakso dan mie ayam serta 6 orang tidak suka keduanya.
Gambarlah diagram venn berdasarkan keterangan di atas.
Berapa banyak anak dalam kelompok tersebut?
SOLUTION:
Diketahui:
bakso ada 45
Mie ayam ada 34
Irisan = 23
X = 6
Dit:
Diagram venn
S.
Isikan terlebih dahulu irisannya yaitu 23.
n (bakso) diisi dengan 45-23 =
22.
n (mie ayam)diisi dengan 34-23 = 11.
X = 6
S = 22 + 23 + 11 + 6 = 62.Berarti banyak anak dalam kelompok tersebut ada 62 orang.
3. Dalam suatu kelas terdapat 48 siswa.
Ternyata 29 siswa gemar matematika, 27 siswa gemar fisika, dan 6 siswa tidak menggemari kedua pelajaran tersebut.
Gambarlah diagram venn dari keterangan di atas.
Tentukan banyaknya siswa yang gemar matematika dan fisika.
SOLUTION:
Diketahui:
S = 48
Matematika ada 29
Fisika ada 27
X = 6
Dit:
Diagram venn
Irisan ( I).
S =48
Isikan terlebih dahulu irisannya yaitu I
n (mtk) diisi dengan 29-I .
n (fisika)diisi dengan 27-I.
X = 6
29-I + I + 27- I + 6 = 48.
29 + 27 + 6 – I = 48
62 – I = 48
I = 62- 48 = 14
Smart Solution:
I = (29 + 27 +6 )-48
I = 62-48 = 14
4. Dari sekelompok anak yang banyaknya 60 orang, diantaranya 50 anak gemar basket, 40 orang anak gemar bulutangkis, dan 35 anak gemar kedua-duanya.
a. Buatlah diagram venn berdasarkan keterangan di atas!
b. Berapa anak yang tidak gemar basket maupun bulutangkis?
SOLUSI:
dik:
S = 60
Basket ada 50
Bulu Tangkis 40
Irisan = 35
dit:
a. Diagram Venn
b. X
Untuk menentukan x maka:
x = 60 – (15+35+5)
x = 60-55
x = 5
Bearti banyak anak yang tidak gemar basket dan bulutangkis ada 5 anak.
5. Dari 30 siswa terdapat 25 siswa gemar membaca, 20 siswa gemar menyanyi, dan 4 siswa yang tidak gemar membaca maupun menyanyi.
a. Buatlah diagram venn berdasarkan keterangan diatas.
b. Berapa anak yang gemar kedua-duanya.
SOLUSI:
dik:
S = 30
Membaca ada 25
Menyanyi ada 20
x = 4
dit:
a. diagram venn
b. anak yang gemar kedua-duanya (I)
Untuk mencari I gunakan cara SMART SOLUTION:
I = (25+20+4)-30
I = 19
6. Dari sekelompok siswa terdapat 20 siswa yang gemar bulutangkis, 25 gemar tenis meja, dan 18 siswa gemar kedua-duanya.
a. Buatlah diagram Venn untuk menunjukkan fakta tersebut!
b.Berapa banyak siswa dalam kelompok tersebut?
SOLUSI:
dik:
Bulutangkis ada 20
Tenis Meja ada 25
Irisan = 18
Yang tidak gemar keduanya tidak ada
Bearti x = 0.
dit:
a. Diagram venn
b. S.
Untuk mencari S maka:
S = 2 + 18 + 7 +0
S = 27
Jadi, banyak siswa dalam kelompok tersebut ada 27.
7. Pada sebuah agen koran dan majalah terdapat 30 orang berlangganan koran dan majalah, 40 orang berlangganan koran, dan 15 orang hanya berlangganan majalah.
a. Buatlah diagram Venn-nya.
b. Berapa banyak pelanggan seluruhnya?
SOLUSI:
Irisan = 30
Koran ada 40
Yang hanya majalah = 15, n(majalah) = 15.
Yang tidak berlangganan tidak ada berarti x = 0.
dit:
a. diagram venn
b. S.
S = 10+30+15
S = 55
Jadi, banyak pelanggan seluruhnya ada 55 orang pelanggan.
8. Dari sekelompok siswa yang terdiri dari 35 orang, ternyata 18 orang gemar matematika, 22 orang gemar bahasa inggris, dan 7 orang tidak gemar keduanya.
a. Buatlah diagram Venn berdasarkan keterangan di atas!
b. Berapa orang yang gemar matematika dan bahasa inggris?
SOLUSI:
dik:
S = 35
Matematika ada 18
B.Inggris ada 22
x = 7
dit:
a. diagram venn
b. gemar keduanya berarti I.
Untuk menentukan banyak siswa yg gemar matematika dan bahasa inggris,gunakan SMART SOLUTION.
I = (18+22+7)-35
I = 47-35
I = 8
Jadi, banyak siswa yang gemar keduanya ada 8 siswa.
9.Dalam sebuah kelas terdapat 48 anak. Anak yang gemar Matematika ada 35 anak, yang gemar Fisika 40 anak, dan yang gemar keduanya ada 30 anak. Berapa anak yang tidak gemar Matematika dan Fisika?
SOLUTION:
S = 48
Matematika ada 30.
Fisika ada 40.
Irisan = 30.
dit:
yang tidak gemar keduanya = x.
Untuk mencari x maka:
x = 48-(5+30+10)
x = 48 -45
x = 3
Jadi, banyak anak yang tidak gemar keduanya ada 3 anak.
10.Dari 40 orang anak, ternyata 27 anak suka membaca majalah, 25 anak suka membaca koran, dan 4 anak tidak suka kedua-duanya. Berapa banyak anak yang suka membaca majalah maupun koran?
SOLUTION:
S = 40
Membaca Majalah ada 27
Membaca Koran ada 25
x = 4
dit:
Irisan (I)
Untuk menentukan I,
gunakan SMART SOLUTION:
I = (27+25+4)-40
I = 56-40
I = 16
Jadi, banyak anak yang suka membaca keduanya ada 16 anak.
SOAL DAN PEMBAHASAN KONSEP HIMPUNAN PART III
SOAL TENTANG IRISAN, GABUNGAN, SELISIH DAN KOMPLEMEN PADA HIMPUNAN1. Diketahui:
A = {Bilangan asli kurang dari 10}
B = {Bilangan genap kurang dari 12}
dengan mendaftar anggotanya tentukan:
a. A
b. n ( A
Solusi:
A = { 1,2,3,4,5,6,7,8,9}
B = {2,4,6,8,10}
a. A
b. n (A
2. Diketahui:
P = { x | 1
Q = { x | 2
dengan mendaftar anggotanya, tentukan:
a. P
b. n (P
Solusi:
P = {1,3,5,7,9}
Q = {2,3,5,7,11}
a.
b.
3. Jika K = {Faktor dari 24}
M = {x |
dengan mendaftar anggotanya, tentukan:
a.
b.
Solusi:
K = {1,2,3,4,6,8,12,24}
M = {2,4,6,8,10,12}
a.
={1,3,24}.
b.
={10}.
4. Diketahui: S = {1,2,3,4,5,6,7,8,9,10,11,12,13}
R = { x| 2
T = {1,4,9}.
Dengan mendaftar anggotanya, tentukan:
a.
b.
c.
Solusi:
S= {1,2,3,4,5,6,7,8,9,10,11,12,13}.
R = {2,4,6,8,10,12}
T = {1,4,9}
a.
b.
c.
Soal dan Pembahasan konsep Himpunan Part II
SOAL TENTANG IRISAN, GABUNGAN,SELISIH DAN KOMPLEMEN
1. Diketahui:
A = {Bilangan prima kurang dari 13}
B = {Bilangan ganjil kurang dari 15}
Tentukan:
a. A B
B
b. n( A B).
Solusi:
B).
Solusi:
A = {2,3,5,7,11}
B = {1,3,5,7,9,11,13}
a.A B ={3,5,7,11}
B ={3,5,7,11}
b. n (A B)=4.
B)=4.
2. Diketahui:
C = {x|x<5, x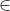 bilangan cacah}
bilangan cacah}
D = {x|x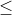 6, x
6, x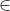 bilangan asli}
bilangan asli}
Tentukan:
a. C D.
D.
b. n (C D).
D).
Solusi:
C = {0,1,2,3,4}
D = {1,2,3,4,5,6}
a. C D = { 1,2,3,4}.
D = { 1,2,3,4}.
b. n (C D)=4.
D)=4.
3. Diketahui:
K = { x| 2 < x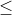 8, x
8, x 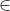 genap}
genap}
L = { x| 2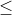 x
x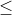 17, x
17, x 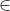 bilangan prima}.
bilangan prima}.
Tentukan K L.
L.
Solusi:
K = {4,6,8}
L = {2,3,5,7,11,13,17}
K L = {}.
L = {}.
4. Diketahui:
K={bilangan cacah kurang dari 6}
L = {bilangan genap kurang dari 10}
Tentukan:
a. K L.
L.
b. n ( K L).
L).
Solusi:
K = {0,1,2,3,4,5}
L = {2,4,6,8}
a. K L = {0,1,2,3,4,5,6,8}
L = {0,1,2,3,4,5,6,8}
b. n (K L)=8.
L)=8.
5. Diketahui:
A = {Bilangan prima kurang dari 7}
B = { x | x < 12, x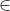 bilangan ganjil}
bilangan ganjil}
C = { X| 2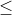 x
x 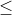 10, x
10, x 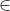 bilangan genap}
bilangan genap}
Tentukan:
a. A B
B
b. B C
C
c. A C
C
d. A B
B  C.
C.
Solusi:
A = {2,3,5}
B = {1,3,5,7,9,11}
C = { 2,4,6,8,10}
a. A B = {1,2,3,5,7,9,11}.
B = {1,2,3,5,7,9,11}.
b. B C ={1,2,3,4,5,6,7,8,9,10,11}
C ={1,2,3,4,5,6,7,8,9,10,11}
c. A C = {2,3,4,5,6,8,10}.
C = {2,3,4,5,6,8,10}.
d. A B
B  C = { 1,2,3,4,5,6,7,8,9,10,11}.
C = { 1,2,3,4,5,6,7,8,9,10,11}.
6. Jika A = {1,2,3} dan B = {3,4,5,6}.Tentukan:
a. A – B
b. B – A
Solusi:
a. A – B = {1,2,3}-{3,4,5,6} = {1,2}
b. B – A = {3,4,5,6}-{1,2,3} = {4,5,6}
7. Jika P = {faktor dari 6} dan Q = { x |-2 < x < 4, x bilangan bulat},tentukan: a. P – Q b. n (P-Q) c. Q – P d. n (Q-P) Solusi: a. P-Q = {1,2,3,6}-{-1,0,1,2,3}={6} b. n (P-Q) =1 c . Q-P = {-1,0,1,2,3}-{1,2,3,6}= {-1,0} d. n (Q-P)= 2 8.Diketahui: S = { 1,2,3,4,5,6,7,8,9,10} A = {2,4,6,8} B = {2,3,5,7} Tentukan: a. Komplemen A b. Komplemen B Solusi: a. Komplemen A artinya anggota di S yang bukan anggota A. Komplemen A = {1,3,5,7,9,10} b. Komplemen B artinya anggota di S yang bukan anggota B. Komplemen B = {1,4,6,8,9,10} 9. Diketahui: S = {1,2,3,4,5,6,7,8,9,10} K = {3,5,6} L = {1,7,8} Tentukan: a. Komplemen K; b. Komplemen L; c. Komplemen K L.
L.
Solusi:
a. Komplemen K = {1,2,4,7,8,9,10}
b. Komplemen L = {2,3,4,5,6,9,10}
c. Komplemen K L = {2,4,9,10}
L = {2,4,9,10}
10.Diketahui:
S = {0,1,2,3,4,5,6,7,8,9,10}
R = {3,6,7,8}
T = {1,2,6,8}
Tentukan Komplemen dari (R T).
T).
Solusi:
R T = {6,8}
T = {6,8}
Komplemen dari (R T) = {0,1,2,3,4,5,7,9,10}
T) = {0,1,2,3,4,5,7,9,10}
11. Jika S ={1,2,3,4,5,6,7,8},A = {1,3,6} dan B = {2,3,6,7},tentukan Komplemen dari (A B).
B).
Solusi:
A B = {1,2,3,6,7}, maka komplemen dari (A
B = {1,2,3,6,7}, maka komplemen dari (A  B)={4,5,8}.
B)={4,5,8}.
12. Jika P = {0,1,2,3,4,5,6,7,8,9,10}, Q = {4,5,6,7,8} dan R = {faktor dari 12},tentukan P ( Q
( Q  R).
R).
Solusi:
Q = {4,5,6,7,8}
R = {1,2,3,4,6,12}
Q R = {1,2,3,4,5,6,8,12}
R = {1,2,3,4,5,6,8,12}
maka P (Q
(Q  R) = {1,2,3,4,5,6,8}.
R) = {1,2,3,4,5,6,8}.
13. Jika A = {1,2,3,4,5}, B = {2,4,6,8} dan C = {3,4,5,6},tentukan (A B)
B)  C.
C.
Solusi:
A B = {1,2,3,4,5,6,8}maka
B = {1,2,3,4,5,6,8}maka
(A B)
B) C = {3,4,5,6}.
C = {3,4,5,6}.
14. Jika A = {2,3,5}, B ={1,3,6,7},dan C = {7,9},tentukan (A B)
B)  (A
(A  C).
C).
Solusi:
A B={1,2,3,5,6,7}.
B={1,2,3,5,6,7}.
A C = {2,3,5,7,9}
C = {2,3,5,7,9}
maka (A B)
B) (A
(A  C)= {2,3,5,7}.
C)= {2,3,5,7}.
15. Jika S = {2,3,4,5,6,7,8}
K = {bilangan prima antara 1 dan 10} dan L = { x| 2< x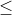 9, x bilangan ganjil},tentukan komplemen dari K
9, x bilangan ganjil},tentukan komplemen dari K  L.
L.
Solusi:
K = {2,3,5,7}
L = {1,3,5,7,9}
K L = {3,5,7} maka Komplemen dari K
L = {3,5,7} maka Komplemen dari K  L ={2,4,6,8,9)
L ={2,4,6,8,9)
1. Diketahui:
A = {Bilangan prima kurang dari 13}
B = {Bilangan ganjil kurang dari 15}
Tentukan:
a. A
b. n( A
A = {2,3,5,7,11}
B = {1,3,5,7,9,11,13}
a.A
b. n (A
2. Diketahui:
C = {x|x<5, x
D = {x|x
Tentukan:
a. C
b. n (C
Solusi:
C = {0,1,2,3,4}
D = {1,2,3,4,5,6}
a. C
b. n (C
3. Diketahui:
K = { x| 2 < x
L = { x| 2
Tentukan K
Solusi:
K = {4,6,8}
L = {2,3,5,7,11,13,17}
K
4. Diketahui:
K={bilangan cacah kurang dari 6}
L = {bilangan genap kurang dari 10}
Tentukan:
a. K
b. n ( K
Solusi:
K = {0,1,2,3,4,5}
L = {2,4,6,8}
a. K
b. n (K
5. Diketahui:
A = {Bilangan prima kurang dari 7}
B = { x | x < 12, x
C = { X| 2
Tentukan:
a. A
b. B
c. A
d. A
Solusi:
A = {2,3,5}
B = {1,3,5,7,9,11}
C = { 2,4,6,8,10}
a. A
b. B
c. A
d. A
6. Jika A = {1,2,3} dan B = {3,4,5,6}.Tentukan:
a. A – B
b. B – A
Solusi:
a. A – B = {1,2,3}-{3,4,5,6} = {1,2}
b. B – A = {3,4,5,6}-{1,2,3} = {4,5,6}
7. Jika P = {faktor dari 6} dan Q = { x |-2 < x < 4, x bilangan bulat},tentukan: a. P – Q b. n (P-Q) c. Q – P d. n (Q-P) Solusi: a. P-Q = {1,2,3,6}-{-1,0,1,2,3}={6} b. n (P-Q) =1 c . Q-P = {-1,0,1,2,3}-{1,2,3,6}= {-1,0} d. n (Q-P)= 2 8.Diketahui: S = { 1,2,3,4,5,6,7,8,9,10} A = {2,4,6,8} B = {2,3,5,7} Tentukan: a. Komplemen A b. Komplemen B Solusi: a. Komplemen A artinya anggota di S yang bukan anggota A. Komplemen A = {1,3,5,7,9,10} b. Komplemen B artinya anggota di S yang bukan anggota B. Komplemen B = {1,4,6,8,9,10} 9. Diketahui: S = {1,2,3,4,5,6,7,8,9,10} K = {3,5,6} L = {1,7,8} Tentukan: a. Komplemen K; b. Komplemen L; c. Komplemen K
Solusi:
a. Komplemen K = {1,2,4,7,8,9,10}
b. Komplemen L = {2,3,4,5,6,9,10}
c. Komplemen K
10.Diketahui:
S = {0,1,2,3,4,5,6,7,8,9,10}
R = {3,6,7,8}
T = {1,2,6,8}
Tentukan Komplemen dari (R
Solusi:
R
Komplemen dari (R
11. Jika S ={1,2,3,4,5,6,7,8},A = {1,3,6} dan B = {2,3,6,7},tentukan Komplemen dari (A
Solusi:
A
12. Jika P = {0,1,2,3,4,5,6,7,8,9,10}, Q = {4,5,6,7,8} dan R = {faktor dari 12},tentukan P
Solusi:
Q = {4,5,6,7,8}
R = {1,2,3,4,6,12}
Q
maka P
13. Jika A = {1,2,3,4,5}, B = {2,4,6,8} dan C = {3,4,5,6},tentukan (A
Solusi:
A
(A
14. Jika A = {2,3,5}, B ={1,3,6,7},dan C = {7,9},tentukan (A
Solusi:
A
A
maka (A
15. Jika S = {2,3,4,5,6,7,8}
K = {bilangan prima antara 1 dan 10} dan L = { x| 2< x
Solusi:
K = {2,3,5,7}
L = {1,3,5,7,9}
K
Soal dan Pembahasan Topik Himpunan
SOAL
1. Di antara kumpulan di bawah ini, manakah yang merupakan himpunan?
a. kumpulan nama planet dalam tata surya.
b. kumpulan hewan berkaki empat.
c. kumpulan makanan yang manis
d. kumpulan ibukota provinsi di Pulau Sumatera.
e. kumpulan makanan yang lezat.
f. kumpulan anak berkulit gelap.
g. kumpulan bilangan prima genap.
h. kumpulan bintang bintang di angkasa.
i. kumpulan warna yang indah.
j. kumpulan penyakit yang diderita manusia.
PEMBAHASAN
a. kumpulan nama planet dalam tata surya.
Keanggotaannya dapat ditentukan dengan jelas, maka kumpulan nama planet dalam tata surya merupakan himpunan.
b. kumpulan hewan berkaki empat.
Keanggotaannya jelas dan ini adalah himpunan.
c. kumpulan makanan yang manis.
Keanggotaannya dapat ditentukan dengan jelas yaitu makanan yang berasa manis seperti kue tart, kue bolu,dodol dan permen.Ini adalah himpunan.
d. kumpulan ibukota propinsi di pulau Sumatera.
Keanggotaanya dapat ditentukan dengan jelas,maka kumpulan ibukota propinsi dipulau sumatera merupakan himpunan.
e. kumpulan makanan yang lezat.
Pengertian lezat tidak jelas batasanya, misalnya rasa (pahit,asam,manis,asin).Dengan demikian,kumpulan makanan yang lezat bukan himpunan.
f. kumpulan anak berkulit gelap.
warna kulit gelap tidak jelas, apakah hitam atau sawo matang.Dengan demikian kumpulan anak berkulit gelap bukan himpunan.
g. kumpulan bilangan prima genap.
anggotanya adalah 2 dan jelas ini adalah himpunan.
h. kumpulan bintang-bintang di angkasa.
Jumlah bintang yang ada di angkasa tidak terdefinisi dengan jelas karena di luar batas kemampuan manusia untuk menjangkaunya, maka ini bukan himpunan.
i. kumpulan warna yang indah.
Pengertian warna yang indah ini tidak jelas karena bergantung pada citarasa dan asumsi masing-masing orang/bersifat relatif.Jadi ini bukan himpunan.
j. kumpulan penyakit yang diderita manusia.
Nama penyakit dan jenisnya tidak jelas, apakah penyakit dalam, penyakit kulit, dan sebagainya. Jadi ini bukan himpunan.
2. P adalah himpunan bilangan genap yang kurang dari 25.
a. Sebutkan anggota-anggota dari P dalam tanda kurung kurawal.
b. Nyatakan P dengan notasi pembentuk himpunan.
c. Tentukan n(P).
Pembahasan:
a. P = {2,4,6,8,10,12,14,16,18,20,22,24}
b. P = {x|x<25, x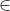 bilangan genap}
bilangan genap}
c. n (P) =12.
3. Tuliskan anggota-anggota yang terdapat di dalam himpunan berikut.
a. P adalah himpunan nama presiden Republik Indonesia.
b. Q adalah himpunan bilangan genap yang kurang dari 10.
c. R adalah himpunan nama pulau besar di Indonesia.
d. S adalah himpunan faktor dari 36 yang kurang dari 20.
e. T adalah himpunan nama benua.
f. U adalah himpunan nama samudera.
g. V adalah himpunan nama bulan yang berjumlah 30 hari.
h. W adalah himpunan hewan pemakan rumput.
i. X adalah himpunan kendaraan beroda empat.
j. Y adalah himpunan nama hari yang diawali dengan huruf S.
Pembahasan:
a. P = {Sukarno, Suharto, B.J. Habibie, Abdurahman Wahid, Megawati Sukarnoputri,Susilo Bambang Yudhoyono}.
b. Q = {2,4,6,8}
c. R = {Papua, Kalimantan,Sumatera, Sulawesi, Jawa}
d. S = {1,2,3,4,6,9,12,18}
e. T = {Asia, Afrika, Eropa, Amerika, Australia}
f. U = {Hindia, Pasifik, Atlantik, Artik}
g. V = {April, Juni, September, November}
h. W = { Sapi,Kuda, Kambing,Kerbau}
i. X = {Sedan, Truk, Bus}
j. Y = {Senin, Selasa, Sabtu}
4. Diantara himpunan-himpunan berikut, manakah yang merupakan himpunan kosong?
a. himpunan bilangan genap di antara 6 dan 8.
b. himpunan bilangan prima diantara 13 dan 19.
c. himpunan bilangan cacah yanh kurang dari 0.
d. himpunan nama bulan yang berjumlah 32 hari.
Pembahasan:
a. Himpuann bilangan genap diantara 6 dan 8.
Urutan bilangan genap = 2,4,6,8,10,…
Diantara 6 dan 8 tidak terdapat bilangan genap melainkan angka7 yaitu bilngan ganjil. Jadi himpunan tersebut adalah himpunan kosong.
b. Himpunan bilangan prima diantara 13 dan 19.
Urutan bilangan antara 13 dan 19.
Urutan bilangan antara 13 dan 19 adalah 14,15,16,17,18.
angka 17 merupakan bilangan prima. Jadi,himpunan bilangan prima diantara 13 dan 19 adalah{17}, bukan himpunan kosong.
c. Himpunan bilangan cacah yang kurang dari 0.
Bilangan cacah yang terkecil adalah 0. Tidak ada bilangan cacah yang kurang dari 0. Jadi, himpunan bilangan cacah yang kurang dari 0 merupakan himpunan kosong.
d. Himpunan nama bulan yang berjumlah hari 32.
Jumlah hari dalam sebulan adalah 28,28,30, atau 31. Tidak ada bulan yang memiliki jumlah hari 32.Jadi, himpunan nama bulan yang berjumlah 32 hari merupakan himpunan kosong.
5. Tentukan 2 himpuan semesta untuk setiap himpunan berikut.
a. A = {Jakarta, Serang, Bandung, Semarang,Yogyakarta, Surabaya}
b. B = {2,4,6,8}
c. C = {Yupiter, Saturnus, Uranus,Neptunus}
Pembahasan:
a. A = {Jakarta, Serang, Bandung, Semarang, Yogyakarta, Surabaya}
Himpunan Semesta dari A dapat berupa:
(i){Nama kota di Pulau Jawa}
(ii){ Nama ibukota propinsi di Pulau Jawa}
b. B = {2,4,6,8}
Himpunan semesta dari B dapat berupa:
(i){Bilangan asli}
(ii){ Bilangan genap yang kurang dari 10}
c. C = {Yupiter, Saturnus, Uranus, Neptunus}
Himpunan semesta dari C dapat berupa:
(i){Nama planet dalam tata surya}
(ii){Nama planet yang berukuran lebih besar daripada Bumi}
6. Diketahui P = {a,b,c,d,e}. Tentukan himpunan bagian dari P yang memiliki:
a. 2 anggota
b. 3 anggota
c. 4 anggota
Jawaban:
a. Himpuanan bagian yang terdiri atas 2 anggota:
{a,b},{a,c},{a,d},{a,e},{b,c},{b,d},{b,e},{c,d},{c,e},{d,e}.
Himpunan bagian yang memiliki 2 anggota ada 10 buah.
b. Himpunan bagian yang terdiri dari 3 anggota:
{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,d,e},{b,c,d},{b,c,e},{b,d,e},{c,d,e}.
Himpunan bagian yang memiliki 3 anggota ada 10 buah.
c. Himpunan bagian yang terdiri dari 4 anggota:
{a,b,c,d},{a,b,c,e},{a,b,d,e},{a,c,d,e},{b,c,d,e}
Himpunan bagian yang memiliki 4 anggota ada 5 buah.
7. Diketahui:
P = {k,l,m,n,o}
Q = {k,l,n}
R = {m,n,q}
S = {m,o}
Dari pertayaan-pertanyaan berikut, manakah yang benar?
a. Q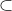 P
P
b. R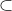 P
P
c. S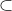 R
R
d. S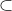 Q
Q
Jawaban:
a. Q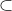 P benar karena setiap anggota Q menjadi anggota P.
P benar karena setiap anggota Q menjadi anggota P.
b. R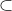 P salah, karena ada anggota R yaiti q yang tidak menjadi anggota P.
P salah, karena ada anggota R yaiti q yang tidak menjadi anggota P.
c. S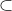 R salah,karena ada anggota S, yaitu o yang tidak menjadi anggota R.
R salah,karena ada anggota S, yaitu o yang tidak menjadi anggota R.
d. S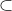 Q benar, karena setiap anggota S menjadi anggota P.
Q benar, karena setiap anggota S menjadi anggota P.
a. kumpulan nama planet dalam tata surya.
b. kumpulan hewan berkaki empat.
c. kumpulan makanan yang manis
d. kumpulan ibukota provinsi di Pulau Sumatera.
e. kumpulan makanan yang lezat.
f. kumpulan anak berkulit gelap.
g. kumpulan bilangan prima genap.
h. kumpulan bintang bintang di angkasa.
i. kumpulan warna yang indah.
j. kumpulan penyakit yang diderita manusia.
PEMBAHASAN
a. kumpulan nama planet dalam tata surya.
Keanggotaannya dapat ditentukan dengan jelas, maka kumpulan nama planet dalam tata surya merupakan himpunan.
b. kumpulan hewan berkaki empat.
Keanggotaannya jelas dan ini adalah himpunan.
c. kumpulan makanan yang manis.
Keanggotaannya dapat ditentukan dengan jelas yaitu makanan yang berasa manis seperti kue tart, kue bolu,dodol dan permen.Ini adalah himpunan.
d. kumpulan ibukota propinsi di pulau Sumatera.
Keanggotaanya dapat ditentukan dengan jelas,maka kumpulan ibukota propinsi dipulau sumatera merupakan himpunan.
e. kumpulan makanan yang lezat.
Pengertian lezat tidak jelas batasanya, misalnya rasa (pahit,asam,manis,asin).Dengan demikian,kumpulan makanan yang lezat bukan himpunan.
f. kumpulan anak berkulit gelap.
warna kulit gelap tidak jelas, apakah hitam atau sawo matang.Dengan demikian kumpulan anak berkulit gelap bukan himpunan.
g. kumpulan bilangan prima genap.
anggotanya adalah 2 dan jelas ini adalah himpunan.
h. kumpulan bintang-bintang di angkasa.
Jumlah bintang yang ada di angkasa tidak terdefinisi dengan jelas karena di luar batas kemampuan manusia untuk menjangkaunya, maka ini bukan himpunan.
i. kumpulan warna yang indah.
Pengertian warna yang indah ini tidak jelas karena bergantung pada citarasa dan asumsi masing-masing orang/bersifat relatif.Jadi ini bukan himpunan.
j. kumpulan penyakit yang diderita manusia.
Nama penyakit dan jenisnya tidak jelas, apakah penyakit dalam, penyakit kulit, dan sebagainya. Jadi ini bukan himpunan.
2. P adalah himpunan bilangan genap yang kurang dari 25.
a. Sebutkan anggota-anggota dari P dalam tanda kurung kurawal.
b. Nyatakan P dengan notasi pembentuk himpunan.
c. Tentukan n(P).
Pembahasan:
a. P = {2,4,6,8,10,12,14,16,18,20,22,24}
b. P = {x|x<25, x
c. n (P) =12.
3. Tuliskan anggota-anggota yang terdapat di dalam himpunan berikut.
a. P adalah himpunan nama presiden Republik Indonesia.
b. Q adalah himpunan bilangan genap yang kurang dari 10.
c. R adalah himpunan nama pulau besar di Indonesia.
d. S adalah himpunan faktor dari 36 yang kurang dari 20.
e. T adalah himpunan nama benua.
f. U adalah himpunan nama samudera.
g. V adalah himpunan nama bulan yang berjumlah 30 hari.
h. W adalah himpunan hewan pemakan rumput.
i. X adalah himpunan kendaraan beroda empat.
j. Y adalah himpunan nama hari yang diawali dengan huruf S.
Pembahasan:
a. P = {Sukarno, Suharto, B.J. Habibie, Abdurahman Wahid, Megawati Sukarnoputri,Susilo Bambang Yudhoyono}.
b. Q = {2,4,6,8}
c. R = {Papua, Kalimantan,Sumatera, Sulawesi, Jawa}
d. S = {1,2,3,4,6,9,12,18}
e. T = {Asia, Afrika, Eropa, Amerika, Australia}
f. U = {Hindia, Pasifik, Atlantik, Artik}
g. V = {April, Juni, September, November}
h. W = { Sapi,Kuda, Kambing,Kerbau}
i. X = {Sedan, Truk, Bus}
j. Y = {Senin, Selasa, Sabtu}
4. Diantara himpunan-himpunan berikut, manakah yang merupakan himpunan kosong?
a. himpunan bilangan genap di antara 6 dan 8.
b. himpunan bilangan prima diantara 13 dan 19.
c. himpunan bilangan cacah yanh kurang dari 0.
d. himpunan nama bulan yang berjumlah 32 hari.
Pembahasan:
a. Himpuann bilangan genap diantara 6 dan 8.
Urutan bilangan genap = 2,4,6,8,10,…
Diantara 6 dan 8 tidak terdapat bilangan genap melainkan angka7 yaitu bilngan ganjil. Jadi himpunan tersebut adalah himpunan kosong.
b. Himpunan bilangan prima diantara 13 dan 19.
Urutan bilangan antara 13 dan 19.
Urutan bilangan antara 13 dan 19 adalah 14,15,16,17,18.
angka 17 merupakan bilangan prima. Jadi,himpunan bilangan prima diantara 13 dan 19 adalah{17}, bukan himpunan kosong.
c. Himpunan bilangan cacah yang kurang dari 0.
Bilangan cacah yang terkecil adalah 0. Tidak ada bilangan cacah yang kurang dari 0. Jadi, himpunan bilangan cacah yang kurang dari 0 merupakan himpunan kosong.
d. Himpunan nama bulan yang berjumlah hari 32.
Jumlah hari dalam sebulan adalah 28,28,30, atau 31. Tidak ada bulan yang memiliki jumlah hari 32.Jadi, himpunan nama bulan yang berjumlah 32 hari merupakan himpunan kosong.
5. Tentukan 2 himpuan semesta untuk setiap himpunan berikut.
a. A = {Jakarta, Serang, Bandung, Semarang,Yogyakarta, Surabaya}
b. B = {2,4,6,8}
c. C = {Yupiter, Saturnus, Uranus,Neptunus}
Pembahasan:
a. A = {Jakarta, Serang, Bandung, Semarang, Yogyakarta, Surabaya}
Himpunan Semesta dari A dapat berupa:
(i){Nama kota di Pulau Jawa}
(ii){ Nama ibukota propinsi di Pulau Jawa}
b. B = {2,4,6,8}
Himpunan semesta dari B dapat berupa:
(i){Bilangan asli}
(ii){ Bilangan genap yang kurang dari 10}
c. C = {Yupiter, Saturnus, Uranus, Neptunus}
Himpunan semesta dari C dapat berupa:
(i){Nama planet dalam tata surya}
(ii){Nama planet yang berukuran lebih besar daripada Bumi}
6. Diketahui P = {a,b,c,d,e}. Tentukan himpunan bagian dari P yang memiliki:
a. 2 anggota
b. 3 anggota
c. 4 anggota
Jawaban:
a. Himpuanan bagian yang terdiri atas 2 anggota:
{a,b},{a,c},{a,d},{a,e},{b,c},{b,d},{b,e},{c,d},{c,e},{d,e}.
Himpunan bagian yang memiliki 2 anggota ada 10 buah.
b. Himpunan bagian yang terdiri dari 3 anggota:
{a,b,c},{a,b,d},{a,b,e},{a,c,d},{a,c,e},{a,d,e},{b,c,d},{b,c,e},{b,d,e},{c,d,e}.
Himpunan bagian yang memiliki 3 anggota ada 10 buah.
c. Himpunan bagian yang terdiri dari 4 anggota:
{a,b,c,d},{a,b,c,e},{a,b,d,e},{a,c,d,e},{b,c,d,e}
Himpunan bagian yang memiliki 4 anggota ada 5 buah.
7. Diketahui:
P = {k,l,m,n,o}
Q = {k,l,n}
R = {m,n,q}
S = {m,o}
Dari pertayaan-pertanyaan berikut, manakah yang benar?
a. Q
b. R
c. S
d. S
Jawaban:
a. Q
b. R
c. S
d. S










Mohon Penjelasan soal no.1
BalasHapus1.Suka tenis 24,tidak suka tenis = 40 - 24 = 26,
2.suka keduanya 11,tidak suka keduanya =40-11=29.
3.Mengapa pernyataan 2 tidak boleh ?